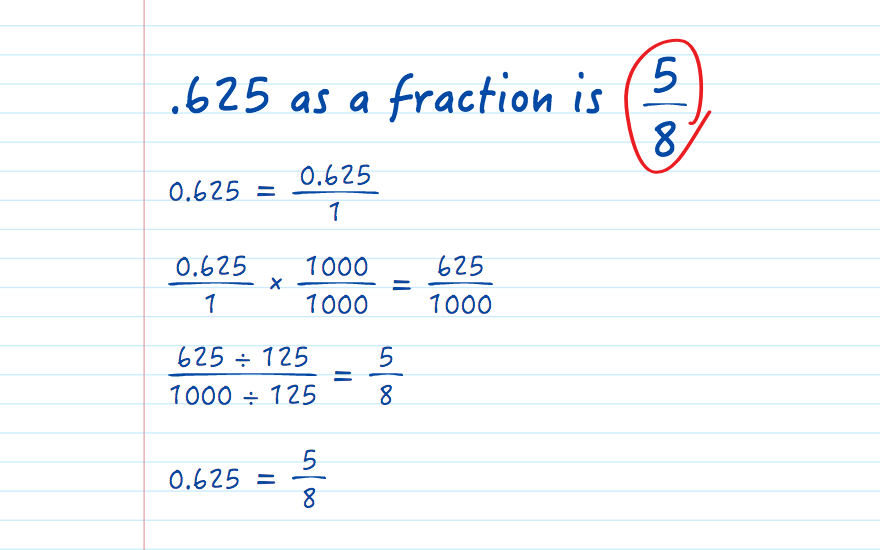Numbers in decimal form are often converted to fractions for precise mathematical calculations. Understanding how to express .625 as a fraction is essential for anyone dealing with mathematics, engineering, or even everyday applications like cooking or construction. This article will delve into the process of converting .625 into a fraction, providing clarity and practical insights.
Converting decimals to fractions is a fundamental concept in mathematics that many people encounter in both academic and real-life scenarios. Whether you're working with measurements, ratios, or proportions, understanding how to convert .625 into a fraction can significantly enhance your problem-solving abilities.
Throughout this guide, we will explore the steps required to convert .625 into its fractional equivalent. Additionally, we will examine various related concepts, such as simplifying fractions, identifying equivalent fractions, and applying this knowledge in practical situations. Let's dive in and unlock the mystery behind .625 as a fraction.
Read also:Marrying Millions Your Ultimate Guide To Love Wealth And Financial Harmony
Table of Contents
- What is a Fraction?
- Converting Decimal to Fraction
- Steps to Convert .625 to a Fraction
- Simplifying the Fraction
- Common Equivalent Fractions
- Real-World Applications
- Tips for Solving Fractions
- Common Mistakes to Avoid
- Advanced Fraction Concepts
- Conclusion and Next Steps
What is a Fraction?
A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts are being considered, while the denominator shows the total number of equal parts the whole is divided into.
For example, in the fraction \( \frac{1}{4} \), the numerator is 1, and the denominator is 4, meaning one part out of four equal parts. Fractions are widely used in mathematics, science, and daily life to represent quantities that are not whole numbers.
Converting Decimal to Fraction
Why Convert Decimals to Fractions?
Decimals and fractions are two ways of representing numbers. While decimals are convenient for some applications, fractions are often preferred for precise calculations. Converting a decimal like .625 into a fraction allows for more accurate mathematical operations and better understanding of numerical relationships.
Basic Principles of Conversion
The process of converting a decimal to a fraction involves identifying the place value of the decimal and expressing it as a fraction. For instance, .625 has three digits after the decimal point, which corresponds to thousandths. This means .625 can initially be written as \( \frac{625}{1000} \).
Steps to Convert .625 to a Fraction
Follow these step-by-step instructions to convert .625 into a fraction:
- Write down the decimal as a fraction: \( \frac{625}{1000} \).
- Simplify the fraction by finding the greatest common divisor (GCD) of 625 and 1000.
- Divide both the numerator and denominator by the GCD to reduce the fraction to its simplest form.
Simplifying the Fraction
Simplification is an essential step in converting decimals to fractions. The fraction \( \frac{625}{1000} \) can be simplified by dividing both the numerator and denominator by their GCD, which is 125. This results in:
Read also:Anthony Kiedis The Controversial Side Of A Music Icon
\( \frac{625 \div 125}{1000 \div 125} = \frac{5}{8} \)
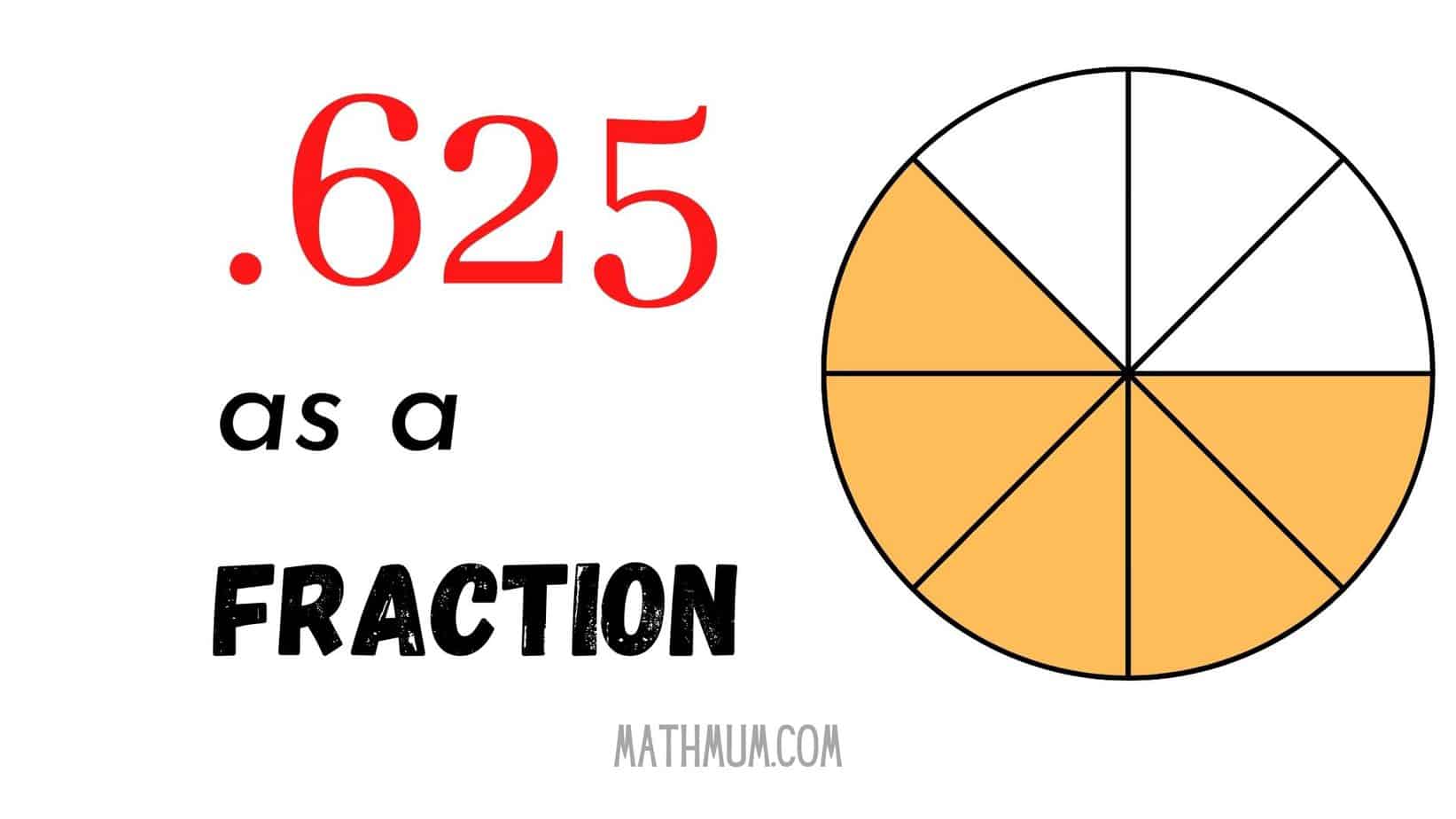
Thus, .625 as a fraction is \( \frac{5}{8} \).
Common Equivalent Fractions
What Are Equivalent Fractions?
Equivalent fractions are fractions that represent the same value but have different numerators and denominators. For example, \( \frac{5}{8} \) is equivalent to \( \frac{10}{16} \), \( \frac{15}{24} \), and so on. These fractions can be obtained by multiplying or dividing both the numerator and denominator by the same number.
Examples of Equivalent Fractions for .625
- \( \frac{10}{16} \)
- \( \frac{15}{24} \)
- \( \frac{20}{32} \)
Real-World Applications
Understanding how to convert .625 into a fraction has practical applications in various fields:
- Cooking: Recipes often require precise measurements, and fractions are commonly used to express ingredient quantities.
- Construction: Builders and architects use fractions to ensure accurate dimensions and measurements.
- Finance: Financial calculations, such as interest rates and investments, frequently involve fractions and decimals.
Tips for Solving Fractions
Useful Strategies
Here are some tips to help you work with fractions effectively:
- Always simplify fractions to their lowest terms for clarity.
- Practice converting decimals to fractions regularly to improve your skills.
- Utilize online calculators or apps for complex fraction problems.
Common Mistakes to Avoid
Pitfalls in Fraction Conversion
When converting decimals to fractions, it's easy to make errors. Here are some common mistakes to watch out for:
- Forgetting to simplify the fraction after conversion.
- Misplacing the decimal point when identifying the place value.
- Incorrectly calculating the GCD, leading to an unsimplified fraction.
Advanced Fraction Concepts
Mixed Numbers and Improper Fractions
Advanced fraction concepts include mixed numbers and improper fractions. A mixed number combines a whole number and a fraction, while an improper fraction has a numerator larger than the denominator. For example, \( \frac{5}{8} \) can be expressed as a mixed number if combined with a whole number.
Operations with Fractions
Fractions can be added, subtracted, multiplied, and divided. Understanding these operations is crucial for solving more complex mathematical problems. For instance, multiplying \( \frac{5}{8} \) by 2 results in \( \frac{10}{8} \), which simplifies to \( \frac{5}{4} \) or \( 1 \frac{1}{4} \).
Conclusion and Next Steps
In conclusion, converting .625 into a fraction is a straightforward process that involves expressing the decimal as \( \frac{625}{1000} \) and simplifying it to \( \frac{5}{8} \). This knowledge is valuable for various applications, from cooking to construction. By following the steps outlined in this guide, you can confidently convert decimals to fractions and simplify them for practical use.
We encourage you to practice converting other decimals to fractions and explore advanced fraction concepts. For further reading, check out our articles on ratios, proportions, and advanced mathematical operations. Don't forget to share this article with others who might find it helpful!